Declaramos la función:

(%i2) f( x) : = x ^ 3 - x ^ 2 + 2 * x + 1 ;
wxplot2d( f( x),[ x, - 2, 2]) ;
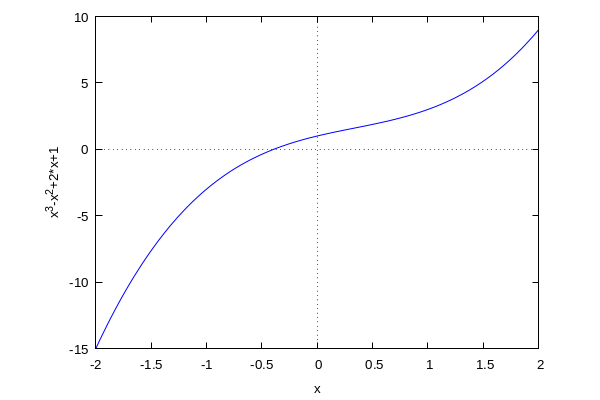
(%o1) f ⁡ ( x ) := x 3 − x 2 + 2 ⁢ x + 1 (%t2) (Gráficos)
(%o2)

Buscamos un intervalo donde se encuentre la raiz, con una longitud pequeña:

(%i4) p : makelist( p, p, - 2, 2, 0 . 5) $
makelist( print( "(", p[ i], ",", f( p[ i]), ")"), i, 1, length( p)) $
( − 2 , − 15 ) ( − 1.5 , − 7.625 ) ( − 1.0 , − 3.0 ) ( − 0.5 , − 0.375 ) ( 0.0 , 1.0 ) ( 0.5 , 1.875 ) ( 1.0 , 3.0 ) ( 1.5 , 5.125 ) ( 2.0 , 9.0 )

Encontramos un cambio de signo en el intervalo [-0.5,0]

1 Método de Newton

A continuación generamos la función a iterar:

(%i5) define( newton( x), x - f( x) / diff( f( x), x)) ;
(%o5) newton ⁡ ( x ) := x − x 3 − x 2 + 2 ⁢ x + 1 3 ⁢ x 2 − 2 ⁢ x + 2

Inicializamos p con el punto medio del intervalo e iteramos. Esta converge hacia un resultado p=newton(p), que es solución de f(x)=0. Veámoslo:

(%i7) p :[( - . 5 + 0) / 2] $
p : append( p,[ float( newton( p[ 1]))]) ;
(p) [ − 0.25 , − 0.4069767441860465 ]

Repetimos la itereción

(%i8) p : append( p,[ float( newton( p[ 1]))]) ;
(p) [ − 0.25 , − 0.4069767441860465 , − 0.4069767441860465 ]

Si consideramos que cometemos un error más pequeño que la diferencia de las dos últimas iteraciones, podemos poner como error:

(%i9) print( "error:", p[ length( p)] - p[ length( p) - 1]) $ ;
error: 0.0

Created with wxMaxima.