Ejer_minimos

Primero visualicemos el problema.

(%i1)

wxdraw2d( implicit( y ^ 2 - 2 * x, x, 0, 2, y, - 2, 2),
   point_type = circle, point_size = 1, points_joined =true, color = red,
   points([[ 1, 1],[ 1, sqrt( 2)]]),
   point_type = circle, point_size = 1, points_joined =true, color = green,
   points([[ 1, 1],[ 0 . 95, sqrt( 2 * 0 . 95)]]),
   point_type = circle, point_size = 1, points_joined =true, color = black,
   points([[ 1, 1],[ 1 . 05, sqrt( 2 * 1 . 05)]])
) ;

\begin{matrix} 0 errores, 0 advertencias \end{matrix}

\begin{matrix} (%t1) \end{matrix}

\begin{matrix} (%o1) \end{matrix}

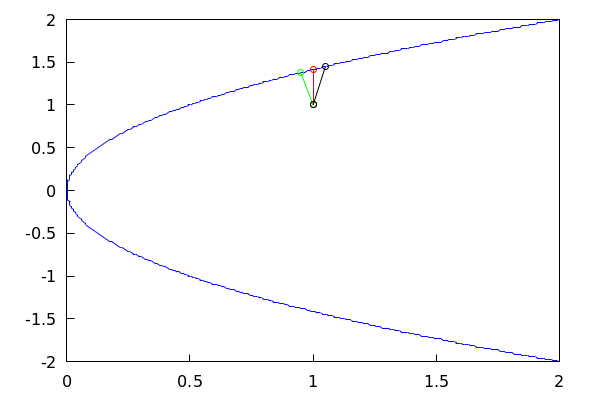
Las lineas verde, roja y negra, nos muestra unos ejemplos de vectores candidatos a solución del problema. Recordemos que la escala de los ejes son diferentes, las apariencias engañan.

Definamos la función que pretendemos minimizar. Esta función será la distancia entre el punto (1,1) y un punto cualquier de la parábola \(y^2=2x\). Como los puntos más cercanos se encuentra en la rama \(y=+\sqrt{2x}\), buscamos la distancia entre (1,1) y \((x,\sqrt{2x})\)

(%i2)

dt( x) : = sqrt(( 1 - x) ^ 2 +( 1 - sqrt( 2 * x)) ^ 2) ;

\begin{matrix} (%o2) & dt (x) := \sqrt{{(1 - x)}^{2} + {(1 - \sqrt{2 x})}^{2}} \end{matrix}

(%i3)

wxplot2d( dt( x),[ x, 0, 2]) ;

\begin{matrix} (%t3) \end{matrix}

\begin{matrix} (%o3) \end{matrix}

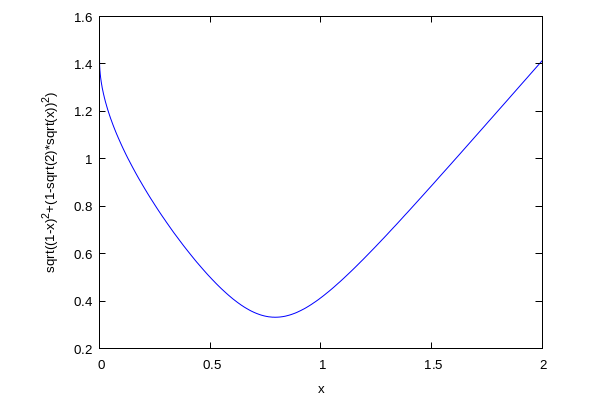
Calculemos la derivada y busquemos sus puntos críticos.

(%i4)

define( Ddt( x), diff( dt( x), x)) ;

\begin{matrix} (%o4) & Ddt (x) := \frac{- 2 (1 - x) - \frac{\sqrt{2} (1 - \sqrt{2} \sqrt{x})}{\sqrt{x}}}{2 \sqrt{{(1 - x)}^{2} + {(1 - \sqrt{2} \sqrt{x})}^{2}}} \end{matrix}

(%i5)

solve( Ddt( x) = 0, x) ;

\begin{matrix} (%o5) & [x = - \frac{2 \sqrt{3} %i + 2}{2^{\frac{7}{3}}}, x = \frac{2 \sqrt{3} %i - 2}{2^{\frac{7}{3}}}, x = \frac{1}{2^{\frac{1}{3}}}] \end{matrix}

Solo nos interesa la coordenada real.

(%i6)

wxdraw2d( implicit( y ^ 2 - 2 * x, x, 0, 2, y, - 2, 2),
point_type = circle, point_size = 1, points_joined =true, color = red,
points([[ 1, 1],[ 1 / 2 ^( 1 / 3), sqrt( 2 / 2 ^( 1 / 3))]])
) ;

\begin{matrix} (%t6) \end{matrix}

\begin{matrix} (%o6) \end{matrix}

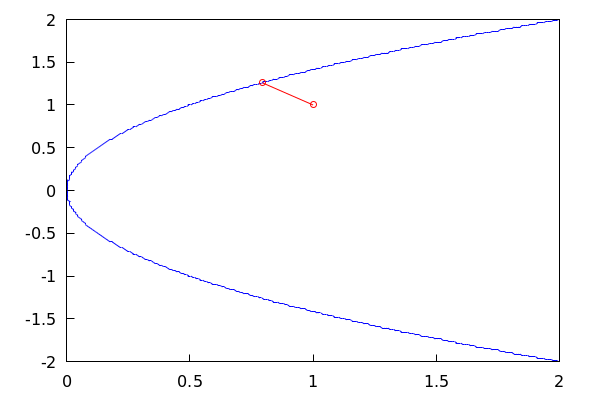
Por tanto la solución será:

(%i7)

sqrt(( 1 / 2 ^( 1 / 3)) ^ 2 +( sqrt( 2 / 2 ^( 1 / 3))) ^ 2) ;

\begin{matrix} (%o7) & \sqrt{2^{\frac{2}{3}} + \frac{1}{2^{\frac{2}{3}}}} \end{matrix}

(%i8)

float( %) ;

\begin{matrix} (%o8) & 1.489080782535197 \end{matrix}

Created with wxMaxima.