El pasado ejercicio, buscábamos los ceros de la segunda derivada de una función para determinar los intervalos donde la función era concava o convexa:

(%i4) f( x) : = x * %e ^( 1 - x ^ 2) $
wxplot2d( f( x),[ x, - 3, 3]) ;
define( df2( x), diff( f( x), x, 2)) ;
wxdraw2d( filled_func =false, fill_color = blue, explicit( df2( x), x, - 3, 3),
   filled_func =false, color = red, line_width = 3, explicit( df2( x), x, 0, 1 . 23),
   filled_func =false, color = red, line_width = 3, explicit( df2( x), x, - 3, - 1 . 23),
   xaxis =true, yaxis =true) ;
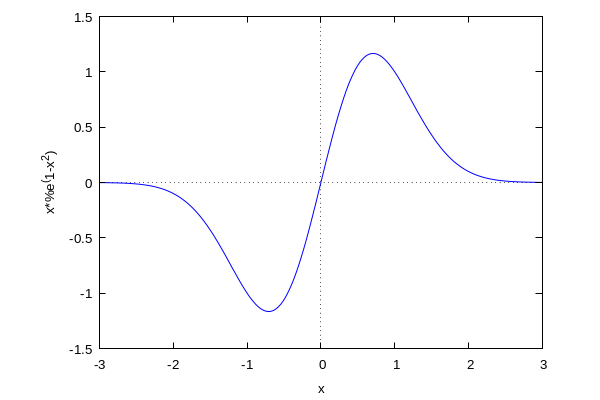
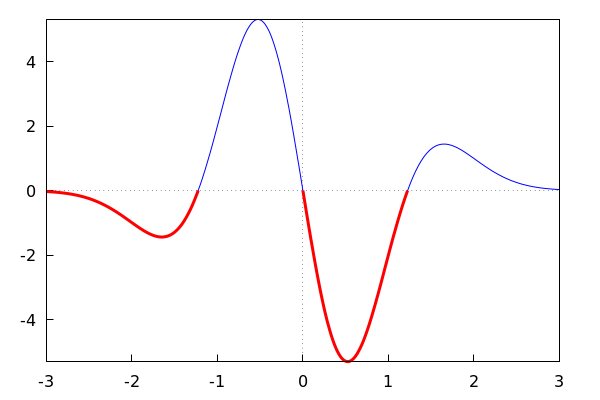
(%t2) (Gráficos)
(%o2) (%o3) df2 ⁡ ( x ) := 4 ⁢ x 3 ⁢ %e 1 − x 2 − 6 ⁢ x ⁢ %e 1 − x 2 0 errores, 0 advertencias (%t4) (Gráficos)
(%o4)

Está claro que x=0 es un cero de df2(x); sin embargo, los otros dos ceros son más difíciles de calcular a simple vista. Veamos como precisamos más con el método de bisección.

Por el teorema de Bolzano, la función si cambia de signo en el intervalo [-1.25,1] tendrá un cero dentro de él:

(%i5) [ df2( - 1 . 25), df2( - 1)] ;
(%o5) [ − 0.178057132728414 , 2 ]

Veamos cómo se comporta en el punto medio:

(%i9) a : - 1 . 25 $ b : - 1 $ p :( a + b) / 2 $
[ df2( a), df2( p), df2( b)] ;
(%o9) [ − 0.178057132728414 , 0.8086569567934427 , 2 ]

Esto significa que el cero se encuentra en el intervalo [a,p]

(%i13) [ a, p] ;
b : p $ p :( a + b) / 2 $
[ df2( a), df2( p), df2( b)] ;
(%o10) [ − 1.25 , − 1.125 ] (%o13) [ − 0.178057132728414 , 0.2831736796689146 , 0.8086569567934427 ]

En cada iteración vamos estrechando el intervalo:

(%i17) [ a, p] ;
b : p $ p :( a + b) / 2 $
[ df2( a), df2( p), df2( b)] ;
(%o14) [ − 1.25 , − 1.1875 ] (%o17) [ − 0.178057132728414 , 0.04395217963578624 , 0.2831736796689146 ]
(%i21) [ a, p] ;
b : p $ p :( a + b) / 2 $
[ df2( a), df2( p), df2( b)] ;
(%o18) [ − 1.25 , − 1.21875 ] (%o21) [ − 0.178057132728414 , − 0.06926069547045 , 0.04395217963578624 ]
(%i25) [ p, b] ;
a : p $ p :( a + b) / 2 $
[ df2( a), df2( p), df2( b)] ;
(%o22) [ − 1.234375 , − 1.21875 ] (%o25) [ − 0.06926069547045 , − 0.01319989042516045 , 0.04395217963578624 ]
(%i29) [ p, b] ;
a : p $ p :( a + b) / 2 $
[ df2( a), df2( p), df2( b)] ;
(%o26) [ − 1.2265625 , − 1.21875 ] (%o29) [ − 0.01319989042516045 , 0.0152405970098286 , 0.04395217963578624 ]

Ya casi tenemos garantizado un decimal exacto.

(%i33) [ a, p] ;
b : p $ p :( a + b) / 2 $
[ df2( a), df2( p), df2( b)] ;
(%o30) [ − 1.2265625 , − 1.22265625 ] (%o33) [ − 0.01319989042516045 , 9.863562344669674 ⁢ 10 −4 , 0.0152405970098286 ]

Como observamos hemos atinado con un p de tres cifras decimales exactas:

(%i34) [ p, df2( p)] ;
(%o34) [ − 1.224609375 , 9.863562344669674 ⁢ 10 −4 ]

Este método es de convergencia lineal. En el próximo veremos como la convergencia es cuadrática, lo que nos llevará a alcanzar más cifras significativas en menos iteraciones.

Created with wxMaxima.