\( \DeclareMathOperator{\abs}{abs} \newcommand{\ensuremath}[1]{\mbox{$#1$}} \)
Ejercicio
| (%i2) |
solve
(
(
1
/
4
)
·
N
·
(
1
−
N
)
−
(
1
/
20
)
·
N
,
N
)
;
float ( % ) ; |
\[\operatorname{ }\left[ N=\frac{4}{5}\operatorname{,}N=0\right] \]
\[\operatorname{ }\left[ N=0.8\operatorname{,}N=0.0\right] \]
| (%i4) |
equ
:
'
diff
(
N
,
t
)
=
(
1
/
4
)
·
N
·
(
1
−
N
)
−
(
1
/
20
)
·
N
;
ode2 ( equ , N , t ) ; |
\[\operatorname{ }\frac{d}{d t} N=\frac{\left( 1-N\right) N}{4}-\frac{N}{20}\]
\[\operatorname{ }5 \log{(N)}-5 \log{\left( 5 N-4\right) }=t+\ensuremath{\mathrm{\% c}}\]
| (%i5) | logcontract ( % / 5 ) ; |
\[\operatorname{ }\log{\left( \frac{N}{5 N-4}\right) }=\frac{t+\ensuremath{\mathrm{\% c}}}{5}\]
| (%i6) | solve ( N / ( 5 · N − 4 ) = %e ^ ( t / 5 + c ) , N ) ; |
\[\operatorname{ }\left[ N=\frac{4 {{\% e}^{\frac{t}{5}+c}}}{5 {{\% e}^{\frac{t}{5}+c}}-1}\right] \]
| (%i7) | load ( drawdf ) $ |
| (%i8) |
wxdrawdf
(
0
.
25
·
y
·
(
1
−
y
)
−
0
.
05
·
y
,
line_width = 3 , color = red , soln_at ( 0 , 1 ) ) ; |
\[\operatorname{ }\]
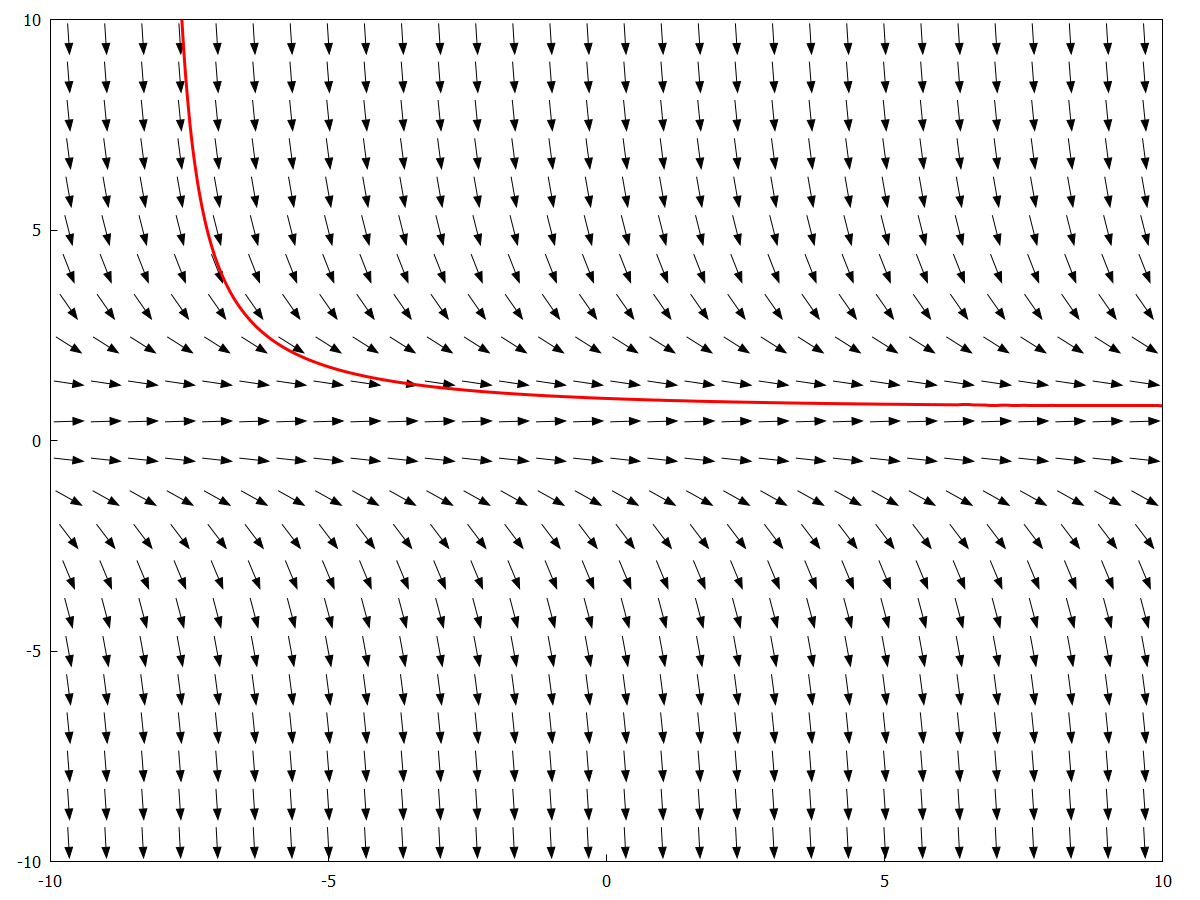
\[\operatorname{ }0\]
Created with wxMaxima.
El modelo original de Levins se aplicó a una metapoblación distribuida en muchos parches(un término fundamental para la ecología del paisaje, se define como una zona relativamente homogénea que difiere de sus alrededores) de hábitat adecuado con una interacción significativamente menor entre parches que dentro de un parche. La dinámica de la población dentro de un parche se simplificó hasta el punto de que sólo se consideró la presencia y la ausencia. Cada parche de su modelo está poblado o no.
Tomemos una fracción los de parches ocupados en un momento dado, dN. Para esa fracción, durante un tiempo dt, cada parche ocupado, N, puede quedar desocupado con un edt de probabilidad de extinción; es decir, eNdt. Adicionalmente, 1-N de los parches están desocupados. Asumiendo una tasa constante c de generación de propágulos de cada una de los N parches ocupadas, durante un tiempo dt, cada mancha desocupada puede llegar a estar ocupada con una probabilidad de colonización cNdt; por tanto, cN(1-N)dt. Si consideramos la tasa de cambio en el tiempo de las manchas ocupadas, dN/dt, donde c=0.25 y e=0.05, ¿cuál de las siguientes constantes es una aproximación a un valor crítico?